Welcome to John Bedini's Web pages.
have moved to www.icehouse.net/john34
This is also the basics for Tesla's
energy shuttle circuits
The two most important electrical energy
statements ever made!!

Gabriel Kron 1901 to 1968
Kron, Gabriel.
"...the missing concept of "open-paths" (the dual of "closed-paths")
was discovered, in which currents could be made to flow in
branches that lie between any set of two nodes. (Previously
— following Maxwell — engineers tied all of their
open-paths to a single datum-point, the 'ground'). That discovery of
open-paths established a second rectangular transformation matrix... which created
'lamellar' currents..." "A network with the simultaneous presence of both closed and
open paths was the answer to the author's years-long search." Gabriel Kron, "The Frustrating Search for a
Geometrical Model of Electrodynamic Networks," Journal unk., issue unk., circa 1962,
p. 111-128. The quote is from p. 114.
Kron, Gabriel. . "When
only positive and negative real numbers exist, it is customary to replace a positive resistance by an inductance and a negative resistance by a capacitor
(since none or only a few negative resistances exist on practical network
analyzers.)" Gabriel Kron,
"Numerical solution of ordinary and partial differential equations by means of
equivalent circuits." Journal of
Applied Physics, Vol. 16, Mar. 1945a, p. 173.
EIGENVALUES AND EIGENFUNCTIONS
Let it be assumed as an example that the V function is a potential well (Fig. 4a). Then in
the network the corresponding positive resistances assume either a constant or a zero
value as shown in Fig. 4b. In practice it is sufficient to extend the network to, say,
twice the width of the potential well on either side.
Let now a d.c.(or a.c.) generator be inserted
anywhere in the network parallel with one of the negative resistances (inductors), as shown. If the values of all the negative
resistances -E?x (capacitors) are simultaneously varied by the same amount, it will be
found that the current (reactive current) in the
generator varies and at some value of E?x becomes zero.
It should be noted that while a current (reactive current) flows in the generator the
circuit does not satisfy the differential equation, since at one point in the
network (where the generator is connected) the currents do not add up to zero (as required
by the equation) but to the generator current. That is, while a current flows in the
generator, the voltages ? do not represent solutions of the differential equation. Hence, only those network conditions are of interest in which the
generator current is zero.
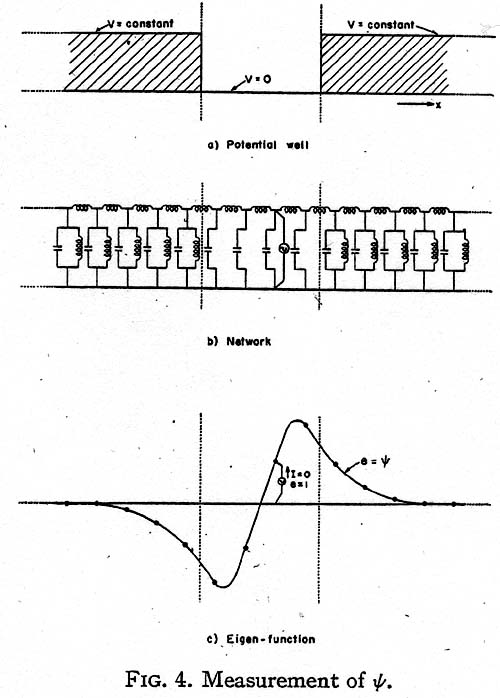
Now a value E of the negative resistances, at which the
generator current becomes zero, represents a state at which the circuit is self-supporting
and has a continuous existence of its own without the presence of the generator,
as the negative resistances just supply the energy consumed by
the positive resistances. (If the circuit contains
inductors and capacitors, the circuit is a resonant circuit and it oscillates at its basic
frequency.) E is then an eigenvalue En, while the voltage distribution
across the capacitors (Fig. 4c) gives the corresponding eigenfunction
?n.
When the generator current is positive the circuit draws energy
from the source, and when the current is negative the circuit pumps back energy into the
source. At zero generator current the circuit neither
gives nor takes energy, and theoretically the generator may be removed. All values
of E at which the current crosses the axes and becomes zero are eigenvalues of the
equation and the corresponding voltage distribution curves are eigenfunctions. When the
energy level E overflows the well, the discrete spectrum of eigenvalues changes into a
continuous spectrum and the generator current is zero at all greater values of E.
When the energy E changes sign, the negative resistances become
positive resistances and at no value of -E may the circuit be self-supporting (as it
contains only positive resistances). That is, the equation has no negative
eigenvalues.
THE STATISTICAL MEAN OF OPERATORS
To bring the measurements at the different energy levels to the same base, it is necessary
to normalize the measured ? values so that the new values of ? satisfy the equation
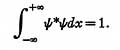
The measured ? functions are normalized by plotting the square of ?. If the area under the
curve is 1/N2, all values of ? are multiplied by N. Then N? is the normalized
?. (Actually N may contain an arbitrary phase ei? .)
The statistical mean of an operator a for a state ? is defined as
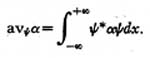
Since (a?x)? is a current (reactive current) flowing through an admittance, ?*(a?x)? is
the power (reactive power) in a single admittance. Hence the total power in a complete set
of similar admittances, namely,
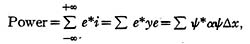
represents the statistical mean of the corresponding energy operator. That is:
1. The total power in all the vertical negative resistors is the average value of
E. (That is, E itself, since ? is an eigenfunction of H).
2. The total power in all the vertical resistors is the average value of the
potential energy V.
3. The total power in all the horizontal resistors is the same as the total
power in the vertical units, representing the average of the kinetic energy T = p2/
2m.
That is, the total power in all positive resistors is the same as the total power in all
the negative resistors, or

THE THIRD MODEL
Let the wave equation be divided by i?c, where ?c = v? = (E/ h)½,
and multiplied by ?x:
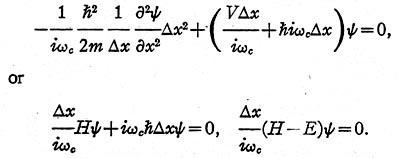
In the present case:
1. The kinetic energy operator T is represented (Fig. 5) by a set of equal
inductors in series, whose inductance L1 is (2m/ h2)?x.
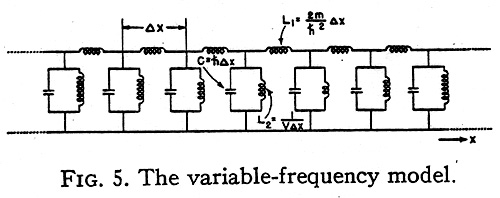
2. The potential energy operator V is represented by a set of unequal coils in
parallel, whose inductance L2 is 1/ V?x.
3. The total energy operator - E is represented by a set of equal capacitors in
parallel whose capacitance is now h?x. (In the second model the capacitance was the
unknown E?x.)
The operand ? is again represented by voltages and the result of the operation a? by the
same currents as in the first model. Their variation in time now is sinusoidal, with 2 p fc
= ?c.
Instead of varying the magnitude of the capacitors, now the
frequency of the generator is varied, thereby varying the admittance of the capacitors, h?c
= E (and those of the inductors). Again when the generator current becomes zero the
circuit is oscillatory and self-supporting and the network represents a stationary
solution of the equation. The corresponding eigenvalue is E = h? = h(?c
)2, rather than h?c, because of the simultaneous variation of the
reactance of the inductive coils. The eigenfunctions ? of the model and of the equation
are, however, identical.
As the currents in the horizontal inductors are (h2/2mi?c )??/ ?x,
the results of an operation on ? by the momentum operator p = (h / i)?/ ?x are these
currents divided by h2/ 2m?c. Hence, in the third model the momentum
operator p may be represented by a set of equal horizontal coils with inductance L = ?x/h?c.
One slight disadvantage of this third model is that as the energy E changes sign, the
reactance of the capacitor j?ch cannot change signs. Since in most cases no
eigenvalues exist in the negative energy range, this disadvantage is of little
consequence. Of course, the second model with fixed frequency and variable capacitors
works in all cases, since the capacitors simply become inductors when E changes sign.
THE FREE PARTICLE IN ONE DIMENSION
An interesting special case occurs when the potential V is zero everywhere. The
one-dimensional equivalent circuit of such a free particle is a conventional transmission
line extending to infinity in both directions (Fig. 6) in which the series inductance is
2m ?x/ h2 and the shunt capacitor is h?x.
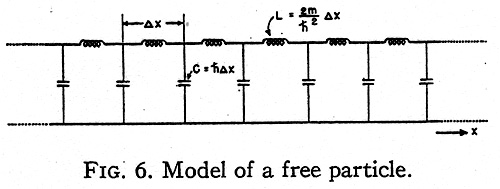
It is well known that such a transmission line may maintain a standing wave at any
frequency ?=?c between zero and infinity drawing no current from the generator.
That is, the positive energy values form a continuous spectrum. If the transmission line
is considered as the second type of model with variable capacitors, then at negative
energy values E the capacitors also become inductors and the line cannot maintain a
standing wave. The corresponding free particle also has no eigenvalue at the negative
energy levels.
MODELS ALONG CURVILINEAR AXES
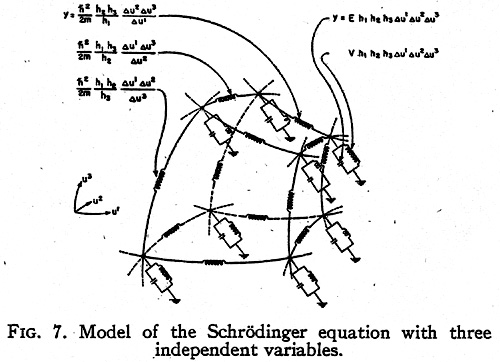
The three-dimensional Schrödinger equation for a single particle is

where ?2 is the Laplacian operator in
curvilinear coordinates.
In order to establish a physical model for it, it is necessary to change it to a tensor
density equation. (2)
The above equation in orthogonal curvilinear coordinates may be changed to a tensor
density form by multiplying it by h1h2h3 = vg giving

If the equation is multiplied through by ?u1?u2?u3, it
represents the surface integral of grad ? around the six faces of a cube of space with
volume h1h2h3?u1?u2?u3.
The width ?ua may be arbitrary and different in the three directions.
The corresponding equivalent circuit is shown in Fig. 7. For a free particle (V=0) it
represents a generalization of the conventional one-dimen- sional transmission line to
three dimensions.
It must be remembered that for a period during the 1960s Kron had refused to publish. Then
he began to publish again, but very cautiously.
Thus he was reluctant to take my advice about the new introduction. During two successive
Saturdays of intensive discussion about this matter he told me that he was leaving his
scientific colleagues behind and entering a new world, that
hisnew discoveries would not be understood unless fully elaborated, and if elaborated
would be plagiarized. In any event, he had no intention of tipping his hand until he had
fully tested his new theories. As I read the new introduction, I find that he temporized.
He did put his work in the perspective of its growth and development and did indicate the
direction in which he was moving, but all in great generalities. These generalities may be
informative, but if they are not then one would have to fall back on a comparison of the
preliminary drafts of the new introduction - if such drafts are still extant.
We know that with the successful development of "Diakoptics"
Gabe turned his attention to new and greater challenges, to the comprehension of phenomena
of a highly complex nature - multidimensional phenomena.
From a philosophical point of view each such phenomenon would be considered complex
because each was conceived as constituting a system not only of manifold
operations, but of manifold heterogeneous operations. The prototype of this
increasingly bold speculation and research was Gabe’s "crystal computer or vest pocket computer," as it
was sometimes jokingly referred to, which utilized the
simultaneous and heterogeneous activity of a crystal under
stimulation of a single electric source. The
important steps here seem to have been the perception of an analogy between the optical
properties of a crystal under stimulation of a single source of light and the mathematical
properties of an electromagnetic field surrounding an electric current, together with the successful use of topology to understand and
manipulate them.
I say that the "crystal computer" constituted a
prototype because I believe this work was successfully accomplished in all its theoretical
aspects long before his death, for Gabriel Kron
showed me what he considered to be proof of the superiority of his new instrument. By this
time, however, something else had entered his mind. I suspect that with the theoretical
background of his work in developing the "crystal computer" it was not a big
jump for the mind of a Gabriel Kron to begin thinking of the universe itself as a
crystal. I also suspect that what he was working
on when he died was a general theory applicable to the universe as a whole system.
After all the universe is a complex phenomenon in which many
heterogeneous activities take place simultaneously. Perhaps Gabe had more
than a vague intuition about short-cuts for interplanetary travel.
But what was Gabriel Kron up too that he was very cautious about?
My pages
 Amplifiers
Amplifiers
 Stubblefield
Stubblefield
 Next PageThis Will Take You To The Energy
Next PageThis Will Take You To The Energy
 Next PageMy 1934 HotRod Ford Pickup page
Next PageMy 1934 HotRod Ford Pickup page




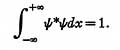
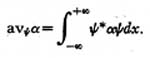

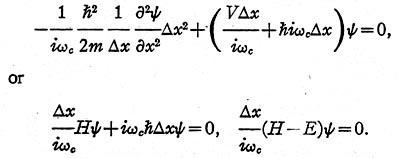





 Next PageThis Will Take You To The Energy
Next PageThis Will Take You To The Energy
 Next PageMy 1934 HotRod Ford Pickup page
Next PageMy 1934 HotRod Ford Pickup page![]()